Algorithm

发表于 2019-05-01 更新于 2024-05-12 分类于算法阅读次数：本文字数： 18k 阅读时长 ≈ 16 分钟

LeetCode 组队刷题活动

组队刷 LeetCode

介绍

代码仓库

　代码仓库的坐标：asdf2014 / algorithm

报名途径

　只需要在《Algorithm》文末的评论区，或者在 issues#40 中留言，即可随时参与

留言内容的话，可以是任意的。另外，也可以说明下自己能接受的刷题频率、希望的选题策略，亦或者，对算法知识沉淀的模式有好的建议，都可以提出，不胜感激

参与方式

　每位参与的小伙伴，都会获得代码仓库的 Collaborator 权限，可以自由地提交代码（不限制语种）。在 /Codes/${你的 Github 账号名} 目录下，每人都将拥有一个自己的代码库。留下 Github 名称后，将很快会收到邀请函，大家可以在 asdf2014 - algorithm - invitations 链接中认领（当然，也欢迎直接通过提交 Pull Request 参与进来）。随后，可以在任意目录下（不需要是空目录），使用如下命令，一键完成你的第一次代码提交：

1	bash -c "$(curl -L https://raw.githubusercontent.com/asdf2014/algorithm/master/first_commit.sh)"

刷题频率

　考虑到可能大家的闲暇时间并不多，我们暂定刷题频率为“一周一题”

选题策略

　选题机器人会在每周五晚八点，自动地随机选定一个题目，当前题目点击这里查看。

其他

　操作 Git 时遇到问题的话，可以参考我的一篇博客《Git 高级玩法》

也可以直接在文章最后留言。目前，支持 Gitalk + Disqus 两种留言系统，以便更好地服务于国内和海外的小伙伴

　同时，为了大家更加方便地交流，也欢迎加入算法 QQ 群或者 Gitter 聊天室

但是，请不要在评论区讨论入群问题的答案，避免打广告的进入

　另外，因为大部分算法都会有很多实现思路，我们会尽可能地展现所有可能的解题方法。但为了文章的排版更加地紧凑，我们会将同一算法的不同实现，通过选项卡的形式展现。且默认展示的选项卡将会是最优解。这样的话，如果你想要快速阅读本文，则可以不用翻看其他的选项卡。实际效果如下：

迭代解

def solution(n):
    if n <= 1:
        return n
    a = 0
    b = 1
    while n > 1:
        n = n - 1
        sum_ = a + b
        a = b
        b = sum_
    return b

递归解

def solution(n):
    if n <= 1:
        return n
    else:
        return solution(n - 1) + solution(n - 2)

动态规划解

def solution(n):
    if n <= 1:
        return n
    cache = [x for x in range(0, n + 1)]
    cache[1] = 1
    for i in range(2, n + 1):
        cache[i] = cache[i - 1] + cache[i - 2]
    return cache[n]

进度

　截止目前为止，活跃的小伙伴数量：，使用到的语言种类：，代码提交频率：，开源许可证：

排行榜

　排行榜的更新会在提交后自动执行，最新的榜单点击这里查看。

下文将总结归纳大家讨论交流的内容，不断地沉淀解题过程中思考的点滴

基础概念

复杂度

Algorithm Complexity

（图片来源：wikipedia.org，已确认版权为 CC BY-SA 4.0 协议）

名称	运行时间	运行时间举例	算法举例
常数时间	$O(1)$	10	判断一个二进制数的奇偶
反阿克曼时间	$O(\alpha (n))$		并查集的单个操作的平摊时间
迭代对数时间	$O(\log ^{\ast}n)$		分布式圆环着色问题
对数对数时间	$O(\log \log n)$		有界优先队列的单个操作
对数时间	$O(\log n)$	$\log n$，$\log n^{2}$	二分搜索
幂对数时间	$(\log n)^{O(1)}$	$(\log n)^{2}$
幂时间（小于 1 次）	$O(n^{c})$，$0<c<1$	$n^{\frac {1}{2}}$，$n^{\frac {2}{3}}$	K-d 树的搜索操作
线性时间	$O(n)$	$n$	无序数组的搜索
线性迭代对数时间	$O(n\log ^ {\ast}n)$		莱姆德·赛德尔的三角分割多边形算法
线性对数时间	$O(n\log n)$	$n\log n$	最快的比较排序
二次时间	$O(n^{2})$	$n^{2}$	冒泡排序、插入排序
三次时间	$O(n^{3})$	$n^{3}$	矩阵乘法的基本实现
多项式时间	$2^{O(\log n)}=n^{O(1)}$	$n$，$n\log n$，$n^{10}$	线性规划中的卡马卡算法，AKS 质数测试
准多项式时间	$2^{(\log n)^{O(1)}}$		关于有向斯坦纳树问题最著名的 $O(\log ^{2}n)$ 近似算法
次指数时间（第一定义）	$O(2^{n^{\epsilon }})$，ε > 0	$O(2^{(\log n)^{\log \log n}})$	假设复杂性理论推测，BPP 包含在 SUBEXP 中
次指数时间（第二定义）	$2^{o(n)}$	$2^{n^{\frac1{3}}}$	用于整数分解与图形同构问题的著名算法
指数时间	$2^{O(n)}$	$1.1^n$，$10^n$	使用动态规划解决旅行推销员问题
阶乘时间	$O(O!)$	$n!$	通过暴力搜索解决旅行推销员问题
指数时间	$2^{poly(n)}$	$2^n, 2^{n^2}$
双重指数时间	$2^{2^{poly(n)}}$	$2^{2^n}$	在预膨胀算术中决定一个给定描述的真实性

（表格来源：wikipedia.org）

经典算法

String Matching

种类

朴素算法（Naive Algorithm）

Rabin-Karp 算法

有限自动机算法（Finite Automation）

KMP

　KMP，Knuth-Morris-Pratt 匹配算法

Boyer-Moore 算法

Simon 算法

Colussi 算法

Galil-Giancarlo 算法

Apostolico-Crochemore 算法

Horspool 算法

Sunday 算法

实战

string-to-integer-atoi

CODE8 1

正则匹配解

import re
patten = '^(([+|-]\\d+)|\\d+)'
def string_to_integer_atoi(s):
    match = re.search(patten, s.strip())
    res = int(match.group()) if match else 0
    return max(min(res, 2 ** 31 - 1), -2 ** 31)

letter-combinations-of-a-phone-number

CODE17 1

算术解

chars = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z" ]

def letter_combinations_of_a_phone_number(digits):
    if len(digits) == 0:
        return []
    if len(digits) == 1:
        return [i for i in letters(digits[0])]
    previous = letter_combinations_of_a_phone_number(digits[:-1])
    return [i + j for i in previous for j in letters(digits[-1])]

def letters(n):
    n = int(n)
    if n < 1 or n > 9:
        return []
    elif n == 1:
        return []
    elif n <= 6:
        return chars[(n - 2) * 3 : (n - 1) * 3]
    elif n == 7:
        return chars[15:19]
    elif n == 8:
        return chars[19:22]
    elif n == 9:
        return chars[22:26]

valid-parentheses

CODE20 1

堆栈解

def valid_parentheses(s: str) -> bool:
    if len(s) == 0 or len(s) % 2 == 1:
        return False
    stack = []
    for c in s:
        if c in revert_pairs.values():
            stack.append(c)
        elif c in revert_pairs:
            if len(stack) == 0 or stack.pop() is not revert_pairs[c]:
                return False
        else:
            return False
    return len(stack) == 0

纯数学解

def zigzag_conversion(s, num_rows):
    s_len = len(s)
    if s_len == 0 or num_rows <= 0:
        return ""
    if s_len < 3 or num_rows == 1:
        return s
    middle_num = num_rows - 2
    cycle_num = num_rows + middle_num
    remain = s_len % cycle_num
    x_total = (s_len // cycle_num) * (middle_num + 1)
    if 0 < remain <= num_rows:
        x_total += 1
    elif remain > num_rows:
        x_total += remain - num_rows + 1
    arr = [["" for _ in range(x_total)] for _ in range(num_rows)]
    count = 0
    for c in s:
        cycle_times = count // cycle_num
        remain = count % cycle_num
        if remain < num_rows:
            arr[remain][cycle_times * (middle_num + 1)] = c
        else:
            arr[num_rows - (remain - (num_rows - 1)) - 1][ cycle_times * (middle_num + 1) + remain - num_rows + 1 ] = c
        count += 1
    return "".join(str(x) for inner_arr in arr for x in inner_arr)

爬格子解

def zigzag_conversion(s, num_rows):
    if num_rows == 1 or num_rows >= len(s):
        return s
    res = [""] * num_rows
    index, step = 0, 1
    for c in s:
        res[index] += c
        if index == 0:
            step = 1
        elif index == num_rows - 1:
            step = -1
        index += step
    return "".join(res)

参考

Book

《柔性字符串匹配》

Sorting Algorithm

排序算法	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
冒泡排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	稳定
选择排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	不稳定
插入排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	稳定
堆排序	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(1)$	不稳定
归并排序	$O(n \log n)$	$O(n \log n)$	$O(n \log n)$	$O(n)$	稳定
快速排序	$O(n \log n)$	$O(n^2)$	$O(n \log n)$	$O(\log n)$	不稳定
希尔排序	$O(n \log^2 n)$	$O(n^2)$	$O(n)$	$O(1)$	不稳定
计数排序	$O(n + m)$	$O(n + m)$	$O(n + m)$	$O(n + m)$	稳定
基数排序	$O(k \times n)$	$O(n^2)$	$O(k \times n)$	$O(n)$	稳定

均按从小到大排列
k：数值中的“数位”个数
n：数据规模
m：数据的最大值减最小值

参考

Dynamic Programming

定义

　动态规划（DP，Dynamic Programming），是一种通过把原问题分解为相对简单的子问题，以求解复杂问题的方法

关键概念

状态

　用来描述该问题的子问题的解

状态转移方程

　状态和状态之间的关系式

　例如，可以将斐波那契数列表示为：

$f(x) = \begin{cases} 0, x = 0 \\ 1, x = 1 \\ f(x - 1) + f(x - 2), x \ge 2, x \in N \end{cases}$

递推

　每个阶段只有一个状态

贪心

　每个阶段的最优状态，都是由上一个阶段的最优状态得到的

搜索

　每个阶段的最优状态，是由之前所有阶段的状态的组合得到的

动态规划

　每个阶段的最优状态，可以从之前某个阶段的某个或某些状态直接得到，而不管之前这个状态是如何得到的

最优子结构

　每个阶段的最优状态，可以从之前某个阶段的某个或某些状态直接得到

无后效性

　不管之前这个状态是如何得到的

实战

longest-palindromic-substring

CODE5 1

S(n) = $O(1)$ 解

def longest_palindromic_substring(s):
    res = ""
    for i in range(len(s)):
        odd = find(s, i, i)
        even = find(s, i, i + 1)
        res = max(res, odd, even, key=len)
    return res

def find(s, left, right):
    while left >= 0 and right < len(s) and s[left] == s[right]:
        left -= 1
        right += 1
    return s[left + 1:right]

regular-expression-matching

CODE10 1

动态规划解

def regular_expression_matching(s, p):
    dp = [[False] * (len(s) + 1) for _ in range(len(p) + 1)]
    dp[0][0] = True
    for i in range(1, len(p)):
        dp[i + 1][0] = dp[i - 1][0] and p[i] == "*"
    for i in range(len(p)):
        for j in range(len(s)):
            if p[i] == "*":
                dp[i + 1][j + 1] = dp[i - 1][j + 1] or dp[i][j + 1]
                if p[i - 1] == s[j] or p[i - 1] == ".":
                    dp[i + 1][j + 1] |= dp[i + 1][j]
            else:
                dp[i + 1][j + 1] = dp[i][j] and (p[i] == s[j] or p[i] == ".")
    return dp[-1][-1]

generate-parentheses

CODE22 1

动态规划解

def generate_parentheses(n: int) -> [str]:
    if n <= 0:
        return []
    res = [[None], ["()"]]
    for i in range(2, n + 1):
        tmp = []
        for j in range(i):
            tmp1 = res[j]
            tmp2 = res[i - j - 1]
            for t1 in tmp1:
                for t2 in tmp2:
                    if t1 is None:
                        t1 = ""
                    if t2 is None:
                        t2 = ""
                    tmp.append("(" + t1 + ")" + t2)
        res.append(tmp)
    return res[n]

参考

Hash

哈希冲突

开放式寻址

线性探测法

从发生冲突的地址起，依次判断下一个地址是否为空，直到碰到空闲的地址
直接定址法

取关键字 $k$ 或者 $k$ 的某个线性函数值（$a \cdot k + b$）作为哈希地址
二次探测法

以关键字 $k$ 或者 $k$ 加上某个常数的平方（$k + 1^2$、$k + 2^2$、$k + 3^2$ $\dots$）作为哈希地址
伪随机数法

采用一个伪随机数当作哈希函数
双重哈希法

双重哈希是用于开放寻址最好的方法之一，散列函数如下：

为了能查找整个散列表，值 $h_2(k)$ 需要与表的大小 $T$ 互质。为确保这一条件成立，可采用以下两种方法
- 取 $T$ 为 2 的幂，并设计一个总产生奇数的 $h_2$
- 取 $T$ 为质数，并设计一个总是产生较 $T$ 小的正整数的 $h_2$

关键字分析

数字分析法

提取关键字中，取值比较均匀的数字作为哈希地址
平方取中法

如果关键字各个部分的分布都不均匀的话，可以先求出它的平方值，然后按照需求取中间的几位作为哈希地址
分段叠加法

按照哈希表地址位数将关键字分成位数相等的几部分，其中最后一部分可以比较短。然后将这几部分相加，舍弃最高进位后的结果，即可作为该关键字的哈希地址

冲突转移

拉链法

拉链法，又称链接地址法，是将哈希值相同的元素构成一个同义词的单链表
公共溢出区

将哈希表分为公共区和溢出区，当发生溢出时，将所有溢出数据统一写入到溢出区

实战

two-sum

CODE1 1

T(n) = S(n) = $O(n)$ 解

def two_sum(nums, target):
    nums_len = len(nums)
    if nums_len < 1:
        return False
    cache = {}
    for i in range(nums_len):
        n = nums[i]
        if n in cache:
            return [cache[n], i]
        else:
            cache[target - n] = i

参考

xxHash: an extremely fast non-cryptographic hash algorithm, working at speeds close to RAM limits

Linked List

种类

单向链表

（图片来源：wikipedia.org，已确认无版权）

快慢指针法

　该方法常用于解决查找单向链表的中点、判断链表是否存在环等问题。大体思路便是，设计一快一慢两个指针，记做 fast 和 slow。同时，控制 fast 的速度是 slow 的两倍（如，fast = fast.next.next; slow = slow.next）。这样，可以保证当 fast 到达链表尾部的时候，slow 刚好在链表中间

双向链表

（图片来源：wikipedia.org，已确认无版权）

循环链表

（图片来源：wikipedia.org，已确认无版权）

性能对比

	Linked list	Array	Dynamic array	Balanced tree	Random access list	Hashed array tree
Indexing	$O(n)$	$O(1)$	$O(1)$	$O(\log n)$	$O(\log n)$	$O(1)$
Insert/delete at beginning	$O(1)$	`N/A`	$O(n)$	$O(\log n)$	$O(1)$	$O(n)$
Insert/delete at end	$O(1)$ when last element is known; $O(n)$ when last element is unknown	`N/A`	$O(1)$ amortized	$O(\log n)$	$O(\log n)$ updating	$O(1)$ amortized
Insert/delete in middle	search time + $O(1)$	`N/A`	$O(n)$	$O(\log n)$	$O(\log n)$ updating	$O(n)$
Wasted space (average)	$O(n)$	`0`	$O(n)$	$O(n)$	$O(n)$	$O(\sqrt{n})$

（表格来源：wikipedia.org）

实战

add-two-numbers

CODE2 1

T(n) = $O(n)$ 解

def add_two_numbers(left, right):
    carry = 0
    tmp = ListNode(0)
    root = tmp
    while left or right:
        total = carry + left.val + right.val
        left = left.next
        right = right.next
        carry = total // 10
        tmp.next = ListNode(total % 10)
        tmp = tmp.next
    return root.next

remove-nth-node-from-end-of-list

CODE19 1

遍历解

def remove_nth_node_from_end_of_list(head: ListNode, n: int) -> ListNode:
    tmp = head
    count = 0
    while tmp:
        count += 1
        tmp = tmp.next
    n = count + 1 - n
    if n <= 0:
        return head
    if n is 1:
        return head.next
    tmp = head
    for _ in range(n - 2):
        tmp = tmp.next
    tmp.next = tmp.next.next
    return head

merge-two-sorted-lists

CODE21 1

遍历解

def merge_two_sorted_lists(l1: ListNode, l2: ListNode) -> ListNode:
    root = tmp = ListNode(None)
    while l1 is not None or l2 is not None:
        if l2 is None:
            tmp.next = l1
            l1 = l1.next
        elif l1 is None:
            tmp.next = l2
            l2 = l2.next
        else:
            if l1.val < l2.val:
                tmp.next = l1
                l1 = l1.next
            else:
                tmp.next = l2
                l2 = l2.next
        tmp = tmp.next
    return root.next

Sliding Window

说明

　滑动窗口算法，主要用于解决数组或者字符串的子元素问题。它可以将嵌套的循环问题，转换为单循环问题，从而降低时间复杂度

实战

longest-substring-without-repeating-characters

CODE3 1

T(n) = S(n) = $O(n)$ 解

def longest_substring_without_repeating_characters(s):
    begin = 0
    res = 0
    cache = {}
    for i, c in enumerate(s):
        if c in cache and begin <= cache[c]:
            begin = cache[c] + 1
        else:
            res = max(res, i - begin + 1)
        cache[c] = i
    return res

Math

实战

reverse-integer

CODE7 1
CODE7 2

纯数学的方式

def reverse_integer(x):
    sign = (x > 0) - (x < 0)
    x *= sign
    size = len(str(x))
    res = 0
    for i in range(1, size + 1):
        remaining = x % 10
        refactor = 10 ** (size - i)
        res += remaining * refactor
        x //= 10
    if res > 2 ** 31 - 1:
        return 0
    return sign * res

字符串切片

def reverse_integer(x):
    sign = (x > 0) - (x < 0)
    res = int(str(x * sign)[::-1])
    return sign * res * (res < 2 ** 31)

palindrome-number

CODE9 1
CODE9 2

纯数学的方式

def palindrome_number(x):
    if x < 0:
        return False
    elif x == 0:
        return True
    h, rev = x, 0
    while h:
        rev = rev * 10 + h % 10
        h //= 10
    return rev == x

字符串反转

1 2	def palindrome_number(x): return x == 0 or (x > 0) and int(str(x)[::-1]) == x

roman-to-integer

CODE13 1
CODE13 2

纯数学的方式

d = {"I": 1, "V": 5, "X": 10, "L": 50, "C": 100, "D": 500, "M": 1000}
def roman_to_integer(s):
    res = 0
    high = -1
    for c in reversed(s):
        now = d[c]
        if now < high:
            res -= now
        else:
            res += now
        high = max(high, now)
    return res

字符串替换

d = {"I": 1, "V": 5, "X": 10, "L": 50, "C": 100, "D": 500, "M": 1000}
def roman_to_integer(s):
    res = 0
    s = s.replace("IV", "IIII").replace("IX", "VIIII")
    s = s.replace("XL", "XXXX").replace("XC", "LXXXX")
    s = s.replace("CD", "CCCC").replace("CM", "DCCCC")
    for c in s:
        res += d[c]
    return res

3sum

CODE15 1

基于 2sum 的思路

def sum3(nums):
    if len(nums) < 3:
        return []
    nums.sort()
    res = []
    for k, v in enumerate(nums[:-2]):
        if k >= 1 and v == nums[k - 1]:
            continue
        cache = {}
        for n in nums[k + 1:]:
            if n not in cache:
                cache[-v - n] = 1
            else:
                tmp = [v, -v - n, n]
                if tmp not in res:
                    res += [tmp]
    return res

预测算法

简易平均法

算术平均值

加权平均值

$\frac{\sum^{n}_{i = 1}w_ix_i}{\sum^{n}_{i = 1}w_i}$

移动平均法

指数平滑法

参考

线性回归法

分类算法

贝叶斯（Bayes）

描述

$P(B \mid A) = \frac{P(B)\,P(A \mid B)}{P(A)}$

　其中，$P(A \mid B)$ 是在 $B$ 发生的情况下 $A$ 发生的可能性，称为 $A$ 的后验概率。相应的，$P(B \mid A)$ 则称为 $B$ 后验概率；$P(A)$ 是不考虑任何 $B$ 方面的因素下 $A$ 发生的可能性，称为 $A$ 的先验概率（或边缘概率）。相应的，$P(B)$ 则称为 $B$ 的先验概率

种类

特征独立性

　按照特征之间独立性的强弱，可以分为朴素贝叶斯、半朴素贝叶斯、（一般的）贝叶斯等

分布情况

　按照属性和特征的分布情况，又可以分为高斯贝叶斯、多项式贝叶斯、伯努利贝叶斯等

离散程度

　按照训练集的离散程度，还可以分为离散型贝叶斯、连续型贝叶斯、混合型贝叶斯等

编码实战

　The set A contains 30 a and 10 b, and the set B contains 20 a and 20 b, then what is the value of P(A|a)?

situations = dict()


def priori_probability(situation, probability):
    situations[situation] = probability  # P(A), P(B)


def posterior_probability(situation, probability):
    old_prob = situations[situation]
    situations[situation] = old_prob * probability  # P(A)P(a|A), P(B)P(a|B)


def normalize():
    count = 0
    for situation in situations.values():
        count += situation  # P(A)P(a|A) + P(B)P(a|B)
    for situation, probability in situations.items():
        # P(A)P(a|A)/(P(A)P(a|A) + P(B)P(a|B)), P(B)P(a|B)/(P(A)P(a|A) + P(B)P(a|B))
        situations[situation] = situations[situation] / count


def prob(hypothis):
    return situations[hypothis]  # P(A|a), P(B|a)


priori_probability('A', 0.5)  # P(A)=1/2
priori_probability('B', 0.5)  # P(B)=1/2

posterior_probability('A', 0.75)  # P(a|A)=3/4
posterior_probability('B', 0.5)   # P(a|B)=1/2

normalize()
prob = prob('A')  # P(A|a)
print('The probability of getting `a` that belongs to set `A`: %s' % prob)
# P(a|A): 从 A 中获取 a
# P(A|a): 获取 a，并且 a 恰巧是属于 A 的
# 这两个描述的场景完全不同，对应的概率也因而不同

补充

　当存在多个特征变量时，表达式可扩展为

$P(C \mid F_1,\dots,F_n) = \frac{P(C) \, P(F_1,\dots,F_n \mid C)}{P(F_1,\dots,F_n)} = \frac{1}{Z} P(C)\prod_{i=1}^n P(F_i \mid C)$

　其中，$\frac{1}{Z}$ 是一个只与 $F_i$ 相关的缩放因子，且当特征变量的值固定时，$\frac{1}{Z}$ 为常量

支持向量机（SVM）

感知机追求最大程度正确划分，最小化错误，但相对容易造成过拟合
支持向量机追求在大致正确分类的同时，最大化 margin，一定程度上避免了过拟合。但是由于 SVM 是借助二次规划来求解支持向量，而求解二次规划将涉及 m 阶矩阵的计算（m 为样本的个数）。所以当 m 的数目很大时，该矩阵的存储将消耗大量的机器资源，且运算的时间成本也会很高

聚类算法

K-means

介绍

　输入聚类个数 k，以及包含 n 个数据对象的数据库，输出满足方差最小标准 k 个聚类的一种算法

步骤

从 n 个数据对象任意选择 k 个对象作为初始聚类中心
根据每个聚类对象的均值（中心对象），计算每个对象与这些中心对象的距离；并根据最小距离重新对相应对象进行划分
重新计算每个（有变化）聚类的均值（中心对象）
计算标准测度函数，当满足一定条件，如函数收敛时，则算法终止；如果条件不满足则回到第二步

基数估算

非概率算法

BitMap

Roaring Bitmap

Bloom filter

双层字典码

概率算法

Count-Mean-Min Sketch

LogLog Counting

Linear Counting

LogLog Counting

Adaptive Counting

HyperLogLog Counting

m = 2 ^ b  # with b in [4...16]

if m == 16:
    alpha = 0.673
elif m == 32:
    alpha = 0.697
elif m == 64:
    alpha = 0.709
else:
    alpha = 0.7213 / (1 + 1.079 / m)

registers = [0] * m  # initialize m registers to 0

# Construct the HLL structure
for h in hashed(data):
    register_index = 1 + get_register_index(h, b)  # binary address of the rightmost b bits
    run_length = run_of_zeros(h, b)  # length of the run of zeroes starting at bit b+1
    registers[register_index] = max(registers[register_index], run_length)

# Determine the cardinality
DV_est = alpha * m ^ 2 * 1 / sum(2 ^ -register)  # the DV estimate

if DV_est < 5 / 2 * m:  # small range correction
    V = count_of_zero_registers(registers)  # the number of registers equal to zero
    if V == 0:  # if none of the registers are empty, use the HLL estimate
        DV = DV_est
    else:
        DV = m * log(m / V)  # i.e. balls and bins correction

if DV_est <= (1 / 30 * 2 ^ 32):  # intermediate range, no correction
    DV = DV_est
if DV_est > (1 / 30 * 2 ^ 32):  # large range correction
    DV = -2 ^ 32 * log(1 - DV_est / 2 ^ 32)

HyperLogLog++

MinHash

HyperLogLog++ & Inclusion-exculsion principle

HyperLogLog++ & MinHash

参考

Blog

Github

数据库相关

Binary Search

　二分查找（Binary Search，也称折半搜索、对数搜索），是一种在有序数组中查找某一特定元素的搜索算法

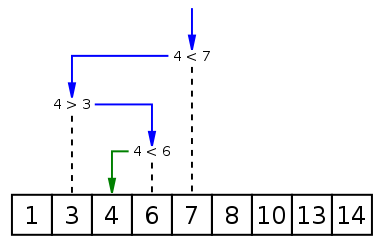
Binary Search

（图片来源：wikipedia.org，已确认无版权）

时间复杂度	T(n) / S(n)
平均	$O(\log n)$
最优	$O(1)$
最坏	$O(\log n)$
最坏	迭代：$O(1)$；递归：$O(\log n)$（无尾调用消除）

实战

median-of-two-sorted-arrays

CODE4 1

Merge Sort 解

def median_of_two_sorted_arrays(nums1, nums2):
    nums = []
    count1 = 0
    count2 = 0
    len1 = len(nums1)
    len2 = len(nums2)
    total_len = len1 + len2
    for i in range(total_len):
        if count1 == len1:
            nums.extend(nums2[count2::])
            break
        if count2 == len2:
            nums.extend(nums1[count1::])
            break
        n1 = nums1[count1]
        n2 = nums2[count2]
        if n1 > n2:
            nums.append(n2)
            count2 += 1
        else:
            nums.append(n1)
            count1 += 1
    middle = total_len // 2
    if total_len % 2 == 0:
        return (nums[middle - 1] + nums[middle]) / 2
    else:
        return nums[middle]

二叉查找树

平衡二叉树

AVL 树

红黑树

B 树

B+ 树

参考

SnapTreeMap

参考

nbronson / snaptree
use SnapTreeMap instead of ConcurrentSkipListMap #6719
Cassandra 2.1: now over 50% faster

LSM tree

参考

前缀树

Tire Tree + Double Array + Aho-Corasick

参考

Patricia Tree

SlimTire

参考

图论

图计算

概念

　图计算是以图论为基础的对现实世界的一种图结构的抽象表达，以及在这种数据结构上的计算模式。通常，在图计算中，基本的数据结构表达就是：

　$G = (V, E, D)$，其中，V = vertex（顶点或者节点），E = edge（边），D = data（权重）

　比如说：对于一个消费者的原始购买行为，有两类节点：用户和产品，边就是购买行为，权重是边上的一个数据结构，可以是购买次数和最后购买时间。对于许多我们面临的物理世界的数据问题，都可以利用图结构的来抽象表达：比如社交网络，网页链接关系，用户传播网络，用户网络点击、浏览和购买行为，甚至消费者评论内容，内容分类标签，产品分类标签等等

加密

GPG

# 安装
$ brew install gpg

# 生成
$ export GPG_TTY=$(tty)
$ gpg --gen-key
$ gpg --list-keys

# 配置
$ git config --global user.signingkey xxx

压缩算法

ZSTD

参考

Zstandard is a real-time compression algorithm, providing high compression ratios

遗传算法

参考

人工智能

　详见，我的另一篇博客《人工智能》

Index

序号	标题	分类
1	Two Sum	Hash
2	Add Two Numbers	Linked List
3	Longest Substring Without Repeating Characters	Sliding Window
4	Median of Two Sorted Arrays	Binary Search
5	Longest Palindromic Substring	Dynamic Programming
6	ZigZag Conversion	String
7	Reverse Integer	Math
8	String to Integer (atoi)	Math & String
9	Palindrome Number	Math
10	Regular Expression Matching	String & Dynamic Programming & Backtracking
11	Container With Most Water	Array & Two Pointers
12	Integer to Roman	Math & String
13	Roman to Integer	Math & String
14	Longest Common Prefix	String
15	3Sum	Array & Two Pointers
16	3Sum Closest	Array & Two Pointers
17	Letter Combinations of a Phone Number	String & Backtracking
18	4Sum	Array & Hash Table & Two Pointers
19	Remove Nth Node From End of List	Linked List & Two Pointers
20	Valid Parentheses	String & Stack
21	Merge Two Sorted Lists	Linked List
22	Generate Parentheses	String & Dynamic Programming & Backtracking